Riddler Classic 6/1/2018
Original post here (fivethirtyeight.com).
From David Seal, a classic construction problem perfect for Infrastructure Week:
Consider four towns arranged to form the corners of a square, where each side is 10 miles long. You own a road-building company. The state has offered you $28 million to construct a road system linking all four towns in some way, and it costs you $1 million to build one mile of road. Can you turn a profit if you take the job?
Extra credit: How does your business calculus change if there were five towns arranged as a pentagon? Six as a hexagon? Etc.?
Answer:
Ollie clarified on Twitter that we should think of the towns as points at the corners of a square:
NOTE: The gridlines represent miles; each side has length 10:
By a kind of heuristic / guessing / iterative reduction method, I found that the shortest graph I could come up with that connects those four points looked like this:
Assuming the four outlying segments have the same length, that length is a function of the length of the center segment.
I tried to come up with y = f(x), where f(x) describes the length of all 5 segments.
y = f(x)=> total length of all segmentsx=> length of center segmentn=> length of outlying segment
From first principles, the length of all sides is 4 * the length of an outlying segment + the length of the center segment:
=> y = 4n + x
To determine n, I tried some example values:
x |
n |
|---|---|
0 |
sqrt(5^2 + 5^2) |
1 |
sqrt(5^2 + (4.5^2) |
2 |
sqrt(5^2 + (4^2) |
From this it became clear that
Plugging that into the original equation for y, we have
Graphing that, courtesy of https://www.desmos.com/calculator:
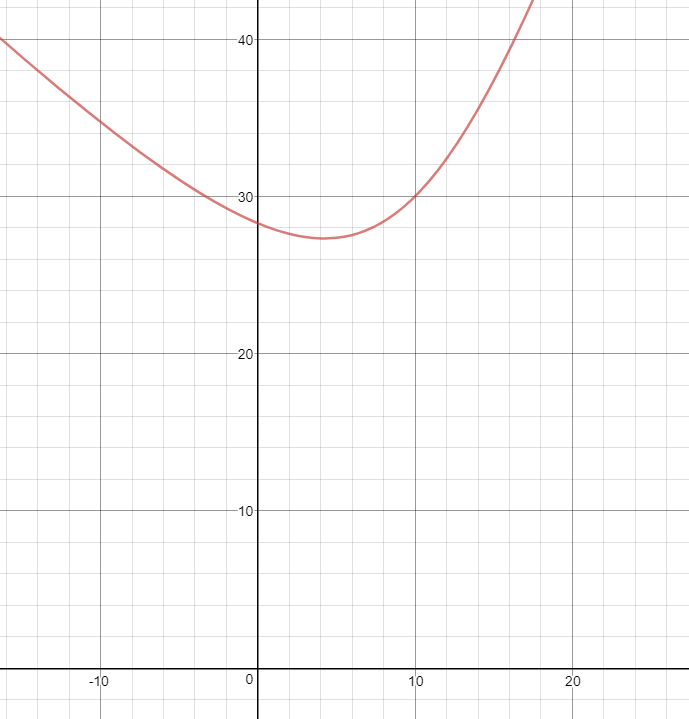
The way to interpret this is is:
-
At
x < 0, the top outlying segments intersect the bottom ones, and the length of the center segment can grow without bound. -
At
x = 0, the center segment degenerates to a point, and the diagram looks like this:
The length here is just over $28m (2 * 10 * sqrt(2)).
- At
x ~ 4, there’s a local minimum and the diagram looks like this:
- At
x = 10, the outlying segments become completely orthogonal to the center segment and the diagram looks like this:
Note that the graph shows y = 30 for x = 10, which is verifiable by inspection.
- At
x > 10, the outlying segments tilt away from the center, and the length of the center segment can grow without bound.
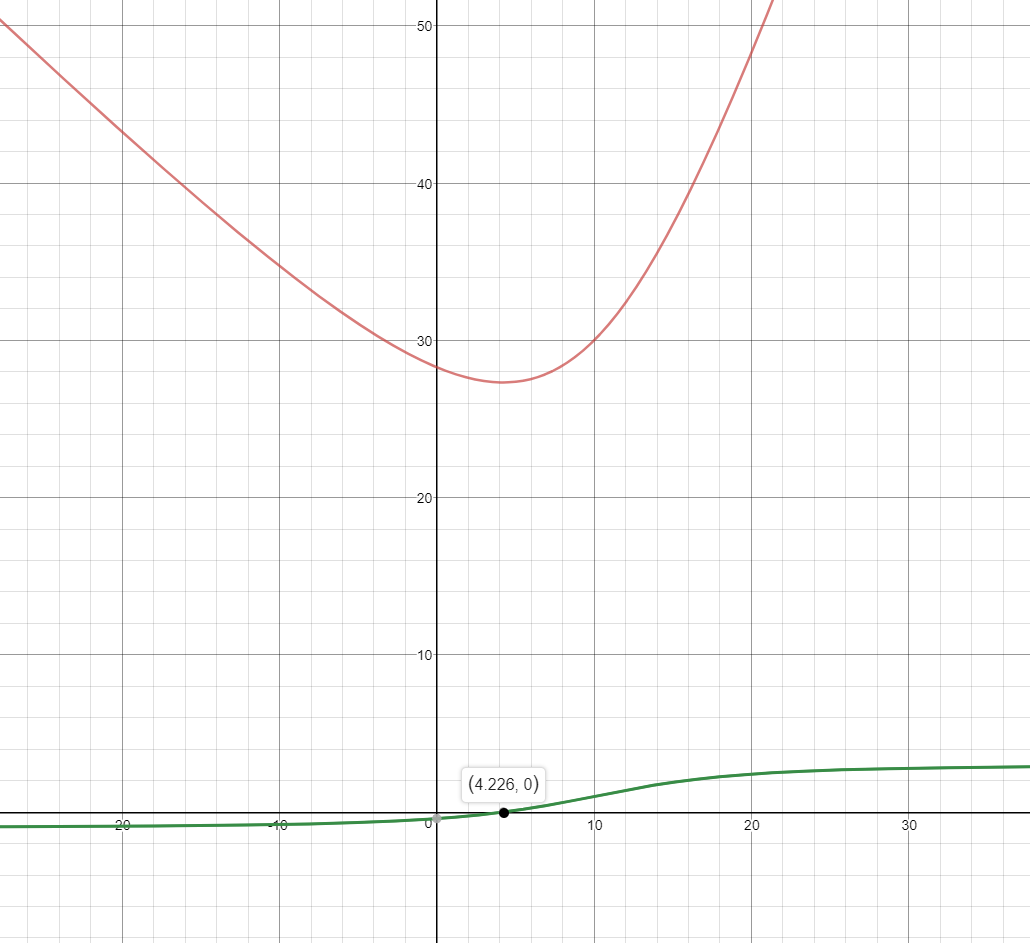
So, there is a minimum in cost at around x ~ 4. To find that mininum, we calculate the derivative of y, y':
Setting that equal to 0 and solving (and graphing) shows that the minimum occurs at x = 4.226:
Plugging x = 4.226 into the original equation for y shows that the minimum cost is y ~ 27.321:
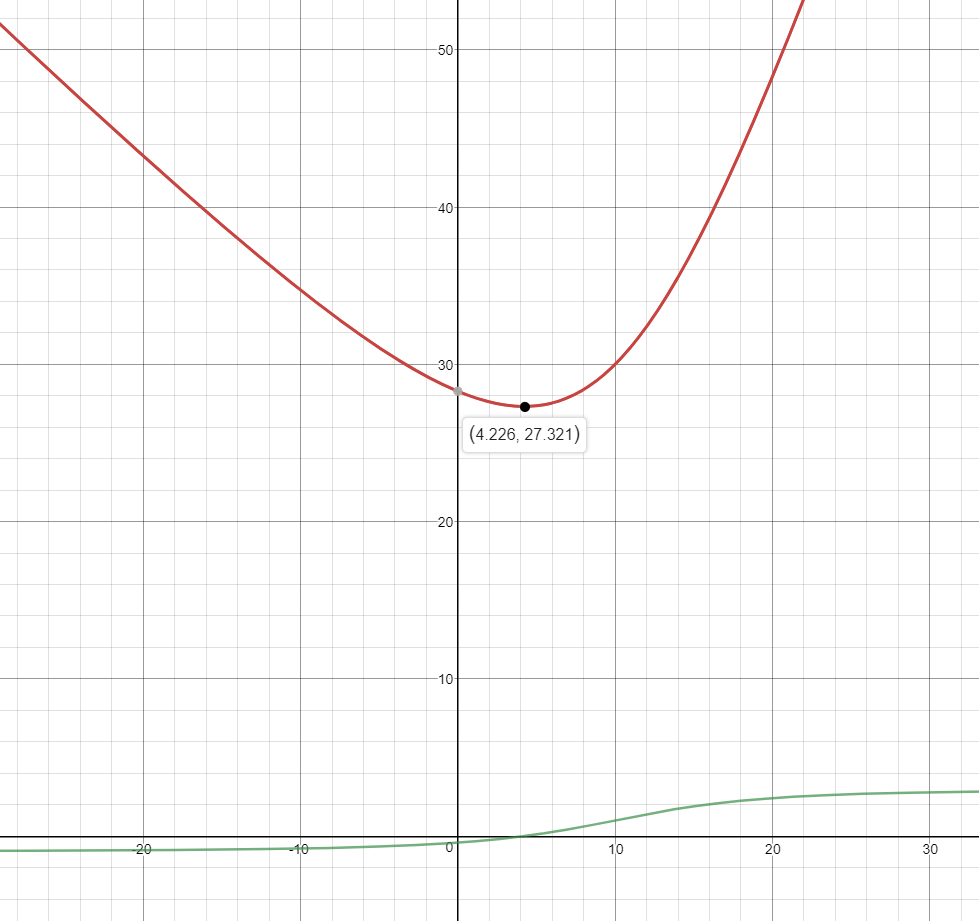
Therefore, since the budget is $28m, we can construct the road at a minimum cost of about $27.321m, which is profitable.